什麼是凱利公式
凱利公式(Kelly Criterion)是一種數學方法,用來幫助交易者與投資人計算「最佳持倉比例」。
這套公式由貝爾實驗室的約翰·L·凱利(John L. Kelly Jr.)於 1956 年提出,目的是最大化資金的長期成長率。
它的原理是根據個人歷史表現與勝率,計算應該投入多少比例的資金於每一筆交易中。
從根本上說,凱利公式追求的是「財富對數的期望值」最大化,而非單純收益最大化。這種設計專注於長期的複利增長,同時降低爆倉或全盤損失的風險。如今,它已成為現代風險管理的核心理論之一,被廣泛應用於交易、體育博弈與投資組合管理。
查看 BTC 在 LBank 的市場表現
BTC()價格
凱利公式解析
凱利公式根據不同情境有兩種計算方式,兩者的目的相同,都是求出 f*,也就是應投入的最適資金比例。
原始凱利公式
在只有兩種結果(贏或輸)的簡單賭局中,公式如下:
f* = (bp - q) / b
其中:
- f* = 應投入的資金比例
- b = 賭注的淨賠率(每投注 1 美元可贏得的淨收益)
- p = 獲勝的概率
- q = 失敗的概率(等於 1 - p)
例如,假設你玩一場擲硬幣遊戲,每下注 1 美元可贏得 2 美元(b = 2),而你有 60% 的勝率(p = 0.6,q = 0.4)。則凱利公式建議:
f* = (2 × 0.6 - 0.4) / 2 = 0.8 / 2 = 0.4,也就是應投入資金的 40%。
交易系統公式
對於具有歷史數據的交易系統,交易者會使用簡化版本:
Kelly Percentage = W - [(1 - W) / R]
其中:
- W = 歷史勝率(贏單佔比)
- R = 平均盈虧比(平均盈利 ÷ 平均虧損)
兩個公式的目標一致,但輸入不同。原始公式需要精確的概率與報酬數據,而交易公式基於實際交易記錄。多數交易者更偏好第二種,因為它可直接由交易日誌計算得出。
歷史與發展時間線
凱利公式的誕生源自一個出人意料的領域——電話工程。以下是它的演進過程:
John L. Kelly Jr. 發表〈A New Interpretation of Information Rate〉
在貝爾實驗室研究電話線雜訊問題時,提出數學基礎,為後來的凱利準則奠定理論根基。
Edward O. Thorp 將凱利公式應用於 21 點
在著作《Beat the Dealer》中運用此理論進行算牌,徹底改變了賭場策略。
金融業開始採用凱利準則
投資組合經理用於倉位規模控制,開啟其在金融領域的應用。
系統化交易者廣泛採納
趨勢追隨與演算法交易者將其納入風險管理核心。
加密貨幣交易者採用凱利公式
數位資產交易者依據市場高波動性,調整並運用改良版凱利策略。
凱利公式從電話線到交易室的演變,展示了數學概念如何在意想不到的領域找到應用。Kelly 最初開發這一公式,是為了解決通信信道中的隨機雜訊問題。他將「賭徒在不完美資訊下下注」的情境,比擬為「電話線上帶雜訊的數據傳輸」。

華倫·巴菲特與查理·蒙格,圖片來源:Robyn Twomey/Redux/laif
使用凱利公式的關鍵人物
Edward O. Thorp 是將凱利公式從學術理論轉化為實際工具的關鍵人物。在成功應用於 21 點賭場後,他將相同原則帶入股票市場。他的對沖基金 Princeton Newport Partners,透過基於凱利倉位配置的策略,在 29 年間實現了年均 19.1% 的報酬率。
華倫·巴菲特與查理·蒙格雖未明確提及凱利公式,但其投資理念與之相符。巴菲特曾表示,他更願意「在少數確信的標的上投入有意義的資金」,而非分散投資過度。這種集中配置的方式正符合凱利數學精神:當你確實擁有優勢時,公式建議加大下注比例。
知名債券投資人比爾·葛羅斯(Bill Gross)也公開承認,他在投資組合配置中參考凱利公式。Kelly 的同事、資訊理論之父 Claude Shannon,也在個人投資中採用此原則。作家 Michael Covel 則透過「TurtleTrader」平台及著作,普及了凱利理念,教導交易者如何根據統計優勢決定倉位大小。
分數凱利策略與風險管理
完整凱利(Full Kelly)在數學上最優,但在實際應用中風險極高。該公式假設你能完全掌握勝率與報酬率,而現實市場遠非如此。若你高估優勢僅 10%,建議倉位可能翻倍,造成巨額回撤。
因此,分數凱利(Fractional Kelly)應運而生,只使用完整凱利的一部分:
- 半凱利(50%):降低約 25% 的波動,只犧牲 25% 的長期增長。
- 四分之一凱利(25%):波動減半,報酬影響極小。
- 十分之一凱利(10%):極度保守,適用於不確定市場。
專業交易者通常使用完整凱利的 10% 至 25%。這種保守方式可防止估算誤差,並在虧損期減輕心理壓力。例如,若完整凱利建議風險資金為 20%,使用四分之一凱利則僅冒 5% 的風險,使資金曲線更平穩,有助交易者在連續虧損時保持紀律。
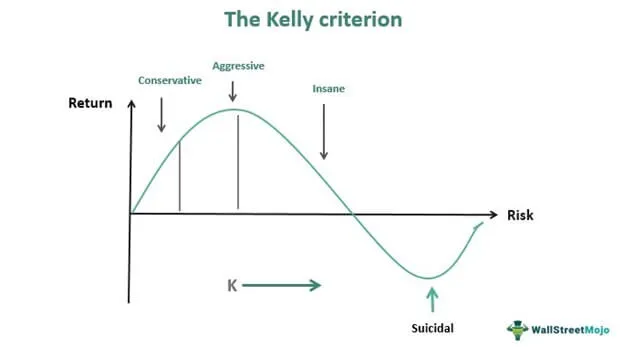
凱利公式,圖片來源:WallstreetMojo
凱利公式 vs 其他投資模型
凱利公式與其他金融模型目的不同。Black-Scholes 用於期權定價,現代投資組合理論(MPT)用於資產配置,而凱利則專注於針對單一機會的倉位大小。
另一個工程數學工具——卡爾曼濾波(Kalman Filter),用於在測量不精確時估計真值。有些交易者會將卡爾曼濾波與凱利結合,前者預測價格變動,後者決定下注金額。
與 MPT 不同,凱利通常獨立評估每筆交易,不考慮資產間的相關性。這讓凱利公式更易實施,但在處理複雜投資組合時略顯簡化。部分量化基金已開發「通用投資組合(Universal Portfolio)」演算法,將凱利理念延伸至多資產同時持倉的場景。
查看 ETH 在 LBank 的市場表現
ETH()價格
將凱利公式應用於加密貨幣交易
加密貨幣市場在實際運用凱利公式時有其獨特挑戰。極端的波動性要求不斷重新計算勝率與持倉規模。以下是一個面向加密交易者的實用框架:
步驟 1:收集歷史數據
追蹤至少 100 筆交易,以建立可靠的勝率與獲利比。由於加密市場變化迅速,應重點關注過去 3 至 6 個月的近期數據,而非多年前的統計。
步驟 2:計算你的優勢
根據你的資料選擇對應公式。若你知道確切的概率與賠率,使用 f* = (bp - q) / b。若你有歷史交易數據,使用 Kelly% = W - [(1-W) / R]。多數加密交易者採用第二個公式,因為它可用實際結果來計算。
步驟 3:採用分數凱利
鑑於加密市場的波動性,切勿使用完整凱利。先從十分之一凱利開始,隨著你對系統的信心提升再逐步增加。
步驟 4:依市場狀況調整
在高波動時期或交易歷史有限的新代幣時縮小持倉規模。對於走勢更可預測的主流幣,則可適度增加持倉。
步驟 5:定期再平衡
每週或每 20 筆交易更新一次你的凱利計算。加密市場演變很快,昨天有效的策略明天可能就不再有效。
真實交易中的限制與風險
交易者必須理解凱利公式存在數個關鍵限制。其一,公式需要準確的概率估計;而在加密市場中,一條推文就可能引發 20% 的價格波動,要計算可靠的概率幾乎不可能。公式也忽略了交易成本,而在加密交易中這些成本可能不少。網路費用、交易所手續費與滑點都會使實際報酬低於理論計算。
心理因素是另一項挑戰。完整凱利的持倉即使在具備正期望值的情況下,也可能帶來超過 50% 的回撤。很少有交易者能承受帳戶腰斬的短暫波動。該公式還假設存在無限多的交易機會,但真實市場中高品質的設定其實有限。
凱利公式也未將黑天鵝事件納入考量——這些罕見但極端的市場波動足以抹去過度槓桿的倉位。在加密市場,這類事件比傳統市場更常見。交易所被駭、監管打擊或技術故障都可能造成凱利計算無法預測的瞬間巨額虧損。
現代應用與工具
當今交易者使用軟體自動執行凱利策略。像 TradingView 和 MetaTrader 這類主流交易平台允許自訂凱利計算器。Python 函式庫(例如 PyPortfolioOpt)也為算法交易者提供凱利優化功能。
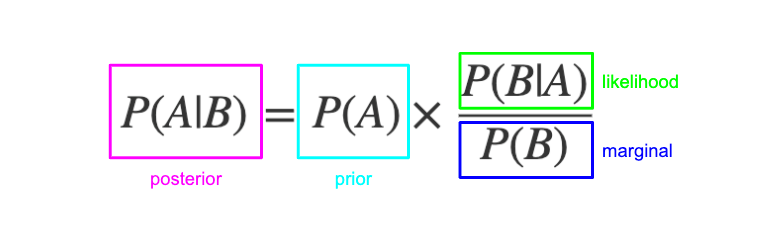
貝葉斯法則,圖片來源:Peter Gleeson
為適應現代市場而衍生的多種改良版本包括:
- 動態凱利:根據市場波動指標調整持倉規模
- 貝葉斯凱利:隨新數據到來更新概率估計
- 帶止損的凱利:在計算中納入最大虧損限制
- 多資產凱利:將公式擴展到整體投資組合的持倉規模
現在也出現了針對加密貨幣的專用工具。3Commas 和 Shrimpy 等平台為加密投資組合提供基於凱利的持倉管理。這些工具會根據近期表現與市場狀況自動調整持倉比例。
實務落地指引
要用好凱利需要紀律與正確執行。先用模擬交易按凱利比例操作,了解系統行為。要詳細記錄每筆交易——公式需要準確的數據才能正確運作。無論凱利建議如何,單一持倉的風險切勿超過 20%。這一道硬性上限能防範計算誤差與黑天鵝事件。
建立系統化的檢視流程。每月或在重大市場變化後重新計算你的凱利百分比。若公式給出負值,立即停止該策略。負的凱利意味著長期期望虧損。在運用凱利時務必考量市場環境。在重大新聞事件、流動性低迷或交易不熟悉資產時縮小持倉;隨著你信心增加並確認你的優勢持續存在,再逐步放大持倉。
記住,凱利優化的是最大化增長,而非最大化安全性。若保本比成長更重要,請使用更小的分數凱利,或乾脆採用其他風險管理方法。最好的持倉管理系統,是能讓你在連勝與連敗時都能持續遵守的那一種。

